Rangkuman Binary tree dan Binary search tree
Binary Tree
Sebelumnya saya sudah membahas tentang Binary Tree, namun kali ini saya akan lebih fokus atau melanjutkan rangkuman materi yang sudah saya bahas sebelumnya. Binary Tree merupakan salah satu bentuk struktur data tidak linear yang menggambarkan hubungan yang bersifat hirarkis (hubungan one to many) antara elemen-elemen. Tree bisa didefinisikan sebagai kumpulan simpul/node dengan satu elemen khusus yang disebut Root dan node lainnya terbagi menjadi himpunan-himpunan yang saling tak berhubungan satu sama lainnya (disebut subtree). Untuk jelasnya, di bawah akan diuraikan istilah-istilah umum dalam tree :
a) Prodecessor : node yang berada diatas node tertentu.
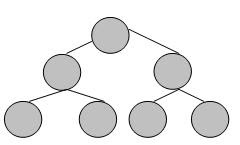 Binary Tree yang tiap nodenya (kecuali leaf) memiliki dua child dan tiap subtree harus mempunyai panjang path yang sama.
Binary Tree yang tiap nodenya (kecuali leaf) memiliki dua child dan tiap subtree harus mempunyai panjang path yang sama.


sumber :
https://abdilahrf.github.io/2015/06/pengenalan-binary-search-tree/
http://new-funday.blogspot.com/2012/12/struktur-data-tree-dan-penjelasaanya.html
http://edyshared.blogspot.com/2013/05/contoh-program-tree-cc.html
Sebelumnya saya sudah membahas tentang Binary Tree, namun kali ini saya akan lebih fokus atau melanjutkan rangkuman materi yang sudah saya bahas sebelumnya. Binary Tree merupakan salah satu bentuk struktur data tidak linear yang menggambarkan hubungan yang bersifat hirarkis (hubungan one to many) antara elemen-elemen. Tree bisa didefinisikan sebagai kumpulan simpul/node dengan satu elemen khusus yang disebut Root dan node lainnya terbagi menjadi himpunan-himpunan yang saling tak berhubungan satu sama lainnya (disebut subtree). Untuk jelasnya, di bawah akan diuraikan istilah-istilah umum dalam tree :
a) Prodecessor : node yang berada diatas node tertentu.
b) Successor : node yang berada di bawah node tertentu.
c) Ancestor : seluruh node yang terletak sebelum node tertentu dan terletak pada jalur yang sama.
d) Descendant : seluruh node yang terletak sesudah node tertentu dan terletak pada jalur yang sama.
e) Parent : predecssor satu level di atas suatu node.
f) Child : successor satu level di bawah suatu node.
g) Sibling : node-node yang memiliki parent yang sama dengan suatu node.
h) Subtree : bagian dari tree yang berupa suatu node beserta descendantnya dan memiliki semua karakteristik dari tree tersebut.
i) Size : banyaknya node dalam suatu tree.
j) Height : banyaknya tingkatan/level dalam suatu tree.
k) Root : satu-satunya node khusus dalam tree yang tak punya predecssor.
l) Leaf : node-node dalam tree yang tak memiliki seccessor.
m) Degree : banyaknya child yang dimiliki suatu node.
Beberapa jenis Tree yang memiliki sifat khusus :
1) Binary Tree
Binary Tree adalah tree dengan syarat bahwa tiap node hanya boleh memiliki maksimal dua subtree dan kedua subtree tersebut harus terpisah. Sesuai dengan definisi tersebut, maka tiap node dalam binary tree hanya boleh memiliki paling banyak dua child.
Jenis-jenis Binary Tree :
a) Full Binary Tree
 Binary Tree yang tiap nodenya (kecuali leaf) memiliki dua child dan tiap subtree harus mempunyai panjang path yang sama.
Binary Tree yang tiap nodenya (kecuali leaf) memiliki dua child dan tiap subtree harus mempunyai panjang path yang sama.
Mirip dengan Full Binary Tree, namun tiap subtree boleh memiliki panjang path yang berbeda. Node kecuali leaf memiliki 0 atau 2 child.
c) Skewed Binary Tree
Implementasi Binary Tree
Binary Tree dapat diimplemntasikan dalam Pascal dengan menggunakan double Linked List. Untuk nodenya, bisa dideklarasikan sbb :
Type Tree = ^node;
Node = record
Isi : TipeData;
Left,Right : Tree;
end;
Contoh ilustrasi Tree yang disusun dengan double linked list :
(Ket: LC=Left Child; RC=Right Child)
Operasi-operasi pada Binary Tree :
v Create : Membentuk binary tree baru yang masih kosong.
v Clear : Mengosongkan binary tree yang sudah ada.
v Empty : Function untuk memeriksa apakah binary tree masih kosong.
v Insert : Memasukkan sebuah node ke dalam tree. Ada tiga pilihan insert: sebagai root, left child, atau right child. Khusus insert sebagai root, tree harus dalam keadaan kosong.
v Find : Mencari root, parent, left child, atau right child dari suatu node. (Tree tak boleh kosong)
v Update : Mengubah isi dari node yang ditunjuk oleh pointer current. (Tree tidak boleh kosong)
v Retrieve : Mengetahui isi dari node yang ditunjuk pointer current. (Tree tidak boleh kosong)
v DeleteSub : Menghapus sebuah subtree (node beserta seluruh descendantnya) yang ditunjuk current. Tree tak boleh kosong. Setelah itu pointer current akan berpindah ke parent dari node yang dihapus.
v Characteristic : Mengetahui karakteristik dari suatu tree, yakni : size, height, serta average lengthnya. Tree tidak boleh kosong. (Average Length = [jumlahNodeLvl1*1+jmlNodeLvl2*2+…+jmlNodeLvln*n]/Size)
v Traverse : Mengunjungi seluruh node-node pada tree, masing-masing sekali. Hasilnya adalah urutan informasi secara linier yang tersimpan dalam tree. Adatiga cara traverse : Pre Order, In Order, dan Post Order.
Langkah-Langkahnya Traverse :
Ø PreOrder : Cetak isi node yang dikunjungi, kunjungi Left Child, kunjungi Right Child.
Ø InOrder : Kunjungi Left Child, Cetak isi node yang dikunjungi, kunjungi Right Child.
Ø PostOrder : Kunjungi Left Child, Kunjungi Right Child, cetak isi node yang dikunjungi.
Untuk lebih jelasnya perhatikan contoh operasi-operasi pada Binary Tree berikut ini :
Binary Search Tree (BST)
biasanya memiliki ciri-ciri seperti berikut :
- Setiap node mempunyai value dan tidak ada value yang double
- value yang ada di kiri tree lebih kecil dari rootnya
- value yang ada di kanan tree lebih besar dari rootnya
- kiri dan kanan tree bisa menjadi root lagi atau bisa mempunya child jadi BST ini memiliki sifat ( rekrusif )
Binary Search Tree dalam contoh di atas setiap node memiliki value yang berbeda , dan sesuai dengan ciri-ciri yang di sebutkan di atas Binary Search Tree memiliki 3 oprasi dasar , hampir mirip dengan array keliatannya jadi ada 3 yaitu :
- Find(x) : find value x didalam BST ( Search )
- Insert(x) : memasukan value baru x ke BST ( Push )
- Remove(x) : menghapus key x dari BST ( Delete )
Oprasi: Search BST dengan adanya ciri” atau syarat di dalam BST , maka untuk finding/searching didalam BST menjadi lebih mudah.
Bayangkan kita akan mencari value X.
Bayangkan kita akan mencari value X.
- Memulai Pencarian Dari Root
- Jika Root adalah value yang kita cari , maka berhenti
- Jika x lebih kecil dari root maka cari kedalam rekrusif tree sebelah kiri
- Jika x lebih besar dari root maka cari kedalam rekrusif tree sebelah kanan
Operasi: Insertion BST
Memasukan value (data) baru kedalam BST dengan rekrusif
Bayangkan kita menginsert value x :
Bayangkan kita menginsert value x :
- Dimulai dari root
- jika x lebih kecil dari node value(key) kemudian cek dengan sub-tree sebelah kiri lakukan pengecekan secara berulang ( rekrusif )
- jika x lebih besar dari node value(key) kemudian cek dengan sub-tree sebelah kanan lakukan pengecekan secara berulang ( rekrusif )
- Ulangi sampai menemukan node yang kosong untuk memasukan value X ( X akan selalu berada di paling bawah biasa di sebut Leaf atau daun )
Contoh Insertion :
Kita ingin menambahkan value 35 kedalam BST yang sudah ada
yang berwarna hijau adalah root , setiap menginsert , mencari , atau delete selalu di mulai dari root.
dan new node berwarna orange yang memiliki value 35, kemudian kita cek dengan root(30), maka 30 .. 35 ? karena 30 < 35 maka , node lebih besar dari root kemudian kita arahkan ke sub-tree yang berada di kanan dan kemudian cek ulang kembali
Sekarang kita cek 35 dengan 37 , maka 35 < 37 jadi kita arahkan ke bagian kiri dan kita cek kembali , karena di bagian kiri sudah ada value yaitu 32
kemudian kita cek 32 dengan 35 , ternyata 35 > 32 jadi kita masukan ke kanan , dan ternyata kita sudah menemukan tempat kosong untuk mengisi new node(35) jadi kita masukan 35 di sebelah kanan dari node(32)
Operasi: Delete ( Remove )
akan ada 3 case yang ditemukan ketika ingin menghapus yang perlu diperhatikan :
- Jika value yang ingin dihapus adalah Leaf(Daun) atau paling bawah , langsung delete
- Jika value yang akan dihapus mempunyai satu anak, hapus nodenya dan gabungkan anaknya ke parent value yang dihapus
- jika value yang akan di hapus adalah node yang memiliki 2 anak , maka ada 2 cara , kita bisa cari dari left sub-tree anak kanan paling terakhir(leaf) (kiri,kanan
) atau dengan cari dari right sub-tree anak kiri paling terakhir(leaf) (kanan,kiri)
Contoh Delete
Delete value 21
21 adalah Leaf atau node paling bawah jadi tinggal delete
kita ingin delete node(37) memiliki 2 anak , jadi kita bisa ambil (35 atau 42 ) untuk menggantikan value(37)
Kiri , anak paling kanan atau kanan anak paling kiri
Contoh 3 Delete
Delete value(30) , value 30 adalah root dari BST , memiliki 2 anak sama seperti case sebelumnnya “Kiri , anak paling kanan atau kanan anak paling kiri”.
jadi kita bisa ambil ( 26 atau 31 ) untuk menggantikan root(30)
Berikut adalah contoh implementasi Program Tree pada C :
#include "stdio.h"
#include "conio.h"
typedef struct Node
{int data;
Node *kiri;
Node *kanan;
};
void tambah(Node **root,int databaru)
{
if((*root) == NULL)
{
Node *baru;
baru = new Node;
baru->data = databaru;
baru->kiri = NULL;
baru->kanan = NULL;
(*root) = baru;
(*root)->kiri = NULL;
(*root)->kanan = NULL;
printf("Data bertambah!");
}
else if(databaru < (*root)->data)
tambah(&(*root)->kiri,databaru);
else if(databaru > (*root)->data)
tambah(&(*root)->kanan,databaru);
else if(databaru == (*root)->data)
printf("Data sudah ada!");
}
void preOrder(Node *root)
{
if(root != NULL){ printf("%d ",root->data);
preOrder(root->kiri);
preOrder(root->kanan);
}}
void inOrder(Node *root)
{
if(root != NULL){ inOrder(root->kiri);
printf("%d ",root->data);
inOrder(root->kanan);
}}
void postOrder(Node *root)
{
if(root != NULL){ postOrder(root->kiri);
postOrder(root->kanan);
printf("%d ",root->data);
}}
void main()
{
int c, data;
Node *pohon,*t;
pohon = NULL;
char pil;
do {
clrscr();
printf("1. Tambah\n");
printf("2. Lihat Pre-order\n");
printf("3. Lihat In-order\n");
printf("4. Lihat Post-order\n");
printf("5. Keluar\n");
printf("Silahkan masukkan pilihan anda (1-5)... ");
pil=getche();
if(pil!='1' && pil !='2' && pil !='3' && pil!='4' && pil!='5' )
printf("\n\nAnda salah mengetikkan inputan...\n");
else
{
if(pil=='1')
{
printf("\n");
printf("\nData baru : ");scanf("%d", &data);
tambah(&pohon,data);
}
else
{
if(pil=='2')
{
printf("\n");
if(pohon!=NULL) preOrder(pohon);
else printf("Masih kosong!");
getch();
}
else
{
if(pil=='3')
{
printf("\n");
if(pohon!=NULL) inOrder(pohon);
else printf("Masih kosong!");
getch();
}
else
{
if(pil=='4')
{
printf("\n");
if(pohon!=NULL) postOrder(pohon);
else printf("Masih kosong!");
getch();
}}}
}}}
while(pil!='5');
}
Mungkin hanya ini yang bisa saya sampaikan sekian dan terima kasih :)sumber :
https://abdilahrf.github.io/2015/06/pengenalan-binary-search-tree/
http://new-funday.blogspot.com/2012/12/struktur-data-tree-dan-penjelasaanya.html
http://edyshared.blogspot.com/2013/05/contoh-program-tree-cc.html










Komentar
Posting Komentar