Tugas GSLC Data Structure
Heap dan Tries
dari gambar itu kita dapat memperoleh kata
Heap
Adalah complete binary tree yang berbasis struktur data dan memenuhi aturan heap. Tree pada heap and deap tidak memenuhi aturan BST yang harus terurut secara inorder, yang penting tree tersebut mengikuti aturan heap.
Heap Terbagi menjadi 3 jenis:
MIN
HEAP TREE
Adalah node yang parentnya lebih kecil dari anaknya
tetapi parentnya lebih besar dari rootnya.
Dapat disimpulkan bahwa root adalah bagian terkecil dari Min-Heap.
Contoh:
Cara Insert:
a. Jika min heap(elemen terkecil terletak di root):
a. Masukkan data nya tidak seperti BST , melainkan dengan konsep array, sehingga kekanan terus, lalu kebawah, dst, atau bisa dikatakan bahwa elemen terakhir akan masuk ke index terakhir/menjadi anak paling kanan dan bawah.
b. Data yang diinsert kemudian dibandingkan dengan parentnya, jika lbh kecil maka swap, lakukan terus menerus sampai root atau sampai data baru tersebut lbh besar dr parentnya.
c. Implementasi dengan array, root itu index nya 1, bukan 0.
Perhitungan:
a. Parent(x) = x / 2
b. Left-child(x) = 2 * x
c. Right-child(x) = 2 * x + 1
Cara Delete:
b. Jika min heap(elemen terkecil terletak di root):
a. Maka yang dihapus merupakan rootnya(elemen terkecil).
b. Root yang dihapus tersebut kemudian digantikan oleh data terakhir di nodenya, kemudian data tersebut di downheapmin(jika anak < data tsb, maka tukar,dst sampai mentok dibawah atau node tsb<anaknya).
MAX HEAP TREE
Adalah node yang parentnya lebih
besar dari anaknya tetapi parentnya lebih kecil dari rootnya.
Dapat disimpulkan bahwa root adalah bagian terbesar dari Max-Heap.
Dapat disimpulkan bahwa root adalah bagian terbesar dari Max-Heap.
Contoh:
Cara Insert:
a. Jika max heap(elemen terbesar terletak di root):
a. Masukkan data nya tidak seperti BST , melainkan dengan konsep array, sehingga kekanan terus, lalu kebawah, dst, atau bisa dikatakan bahwa elemen terakhir akan masukk ke index terakhir/menjadi anak paling kanan dan bawah.
b. Data yang diinsert kemudian dibandingkan dengan parentnya, jika lbh besar maka swap, lakukan terus menerus sampai root atau sampai data baru tersebut lbh kecil dr parentnya.
c. Implementasi dengan array, root itu index nya 1, bukan 0.
Perhitungan:
a. Parent(x) = x / 2
b. Left-child(x) = 2 * x
c. Right-child(x) = 2 * x + 1
Cara Delete:
b. Jika max heap(elemen terkecil terletak di root):
a. Maka yang dihapus merupakan rootnya(elemen terbesar).
b. Root yang dihapus tersebut kemudian digantikan oleh data terakhir di nodenya, kemudian data tersebut di downheapmax(jika anak > data tsb, maka tukar,dst), sampai mentok dibawah atau node tsb>anaknya).
MIN MAX HEAP TREE
Sedangkan Min-Max Heap adalah kombinasi dari keduanya. Jadi tiap levelnya akan bergantian antara Min-Heap dan Max-Heap
Contoh:
Cara Insert:
a. Insert di level Min:
- Proses Node baru yang akan dilakukan dipengaruhi oleh lokasi Node baru tersebut.
- Jika Node baru berada di level min, maka bandingkan dengan parentnya.
i. Jika parent < newnode maka swap dan upheapmax dari parentnya (dibandingkan dengan grandparentnya dari posisi newnode setelah swap).
ii. Jika parent > newnode, upheapmin dari posisi newnode (dibandingkan dengan grandparentnya dari posisi newnode).
b. Insert di Level Max:
- Proses Node baru yang akan dilakukan dipengaruhi oleh lokasi Node baru tersebut.
- Jika Node baru berada di level max, maka bandingkan dengan parentnya.
i. Jika parent > newnode maka swap dan upheapmin dari parentnya (dibandingkan dengan grandparentnya dari posisi newnode setelah swap).
ii. Jika parent < newnode, upheapmax dari posisi newnode (dibandingkan dengan grandparentnya dari posisi newnode).
Cara Delete:
a. Nilai yang dihapus diganti oleh data terakhir.
b. Komparasi dengan grandchild baru lakukan komparasi dengan child nya terus menerus.
Tries
Tries (prefix tree) adalah tree struktur data terstruktur yang digunakan untuk menyimpan array asosiatif (string).
Jadi setiap vertex/node merepresentasikan satu huruf.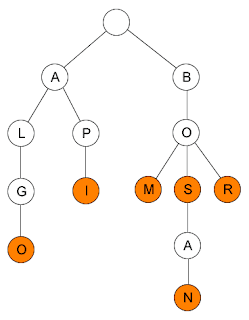 |
1. ALGO
2. API
3. BOM
4. BOS
5. BOSAN
6. BOR
Referensi:





Komentar
Posting Komentar